NAND回路とは、入力条件がすべてONしたときのみ出力条件がOFFする回路です。言い換えると、入力条件のいずれか1ヶでもOFFだと出力条件がONする回路です。
AND回路を反転した回路(NOT AND)であることからNAND回路、もしくは否定論理積回路と呼ばれています。
この記事では、オムロンCJシリーズで作成するNAND(否定論理積)回路のラダープログラム例を2ヶ解説します。
リレー回路で作成するNAND(否定論理積)回路については以下のページで解説しております。
【リレー回路】NAND回路の回路図と動作
三菱電機FXシリーズ・iQ-Fシリーズ・キーエンスKVシリーズで作成するNAND(否定論理積)回路のラダープログラムについては以下のページで解説しております。
【ラダープログラム回路】NAND(否定論理積)回路のラダープログラム例【三菱FX】
【ラダープログラム回路】NAND(否定論理積)回路のラダープログラム例【三菱iQ-F】
【ラダープログラム回路】NAND(否定論理積)回路のラダープログラム例【キーエンスKV】
目次
1.【例題①】入力条件2ヶのNAND回路
下記仕様のラダープログラムを解説します。
スイッチが片方でも放されるとランプは点灯する。
スイッチは押すとON、ランプはONすると点灯するものとする。
2ヶのスイッチを両方押したときのみランプが消灯します。スイッチが片方でも放されているとランプは点灯します。
真理値表
真理値表は以下のようになります。
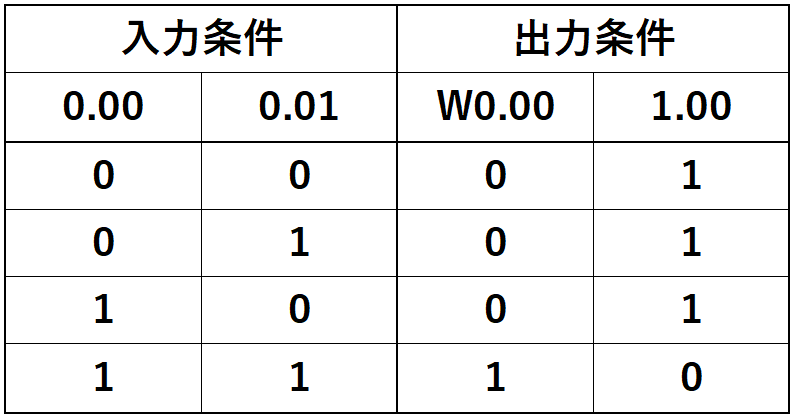
この真理値表では「”1”がON」「”0”がOFF」を表しています。
入力条件0.00と0.01のAND(論理積)がW0.00になります。
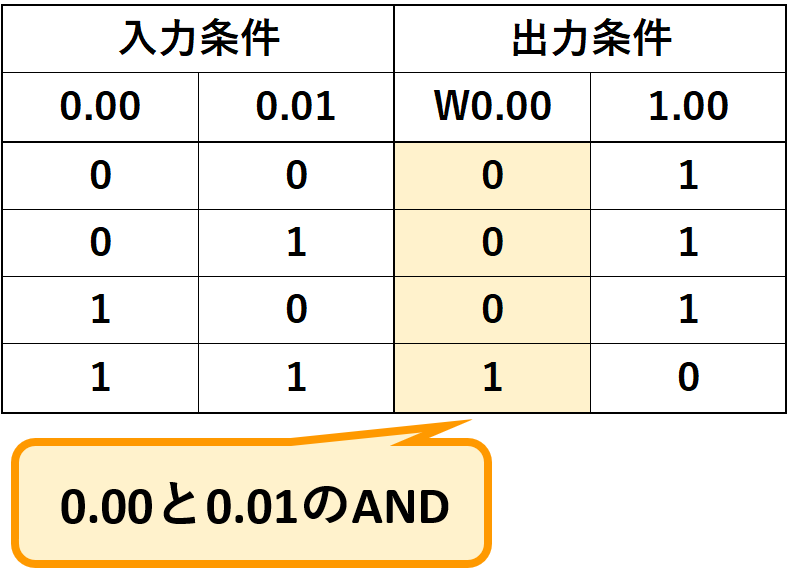
今回求めるNAND(否定論理積)はAND(論理積)を反転したものです。つまり真理値表でW0.00の0と1の状態を反転した結果である1.00がNAND(否定論理積)となります。
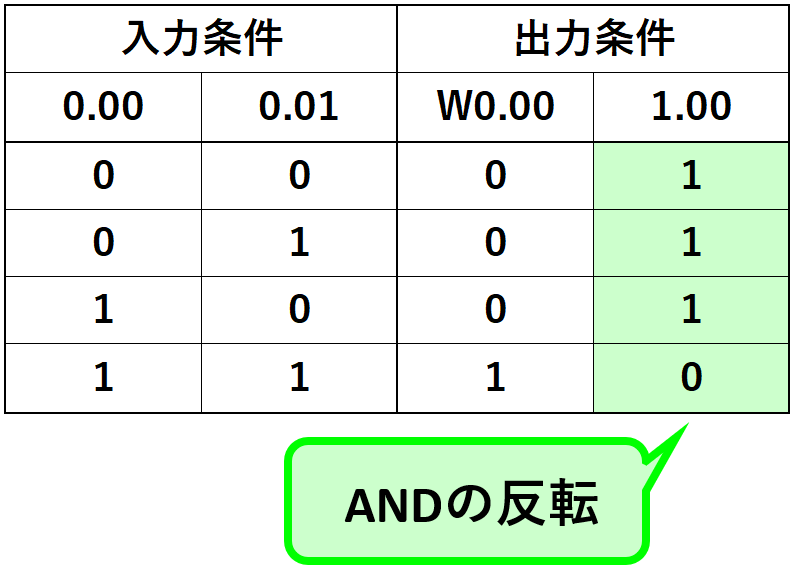
0.00と0.01のNAND(否定論理積)である1.00は、入力条件がどちらも”1”の場合のみ”0”となります。
タイムチャート
タイムチャートは以下のようになります。
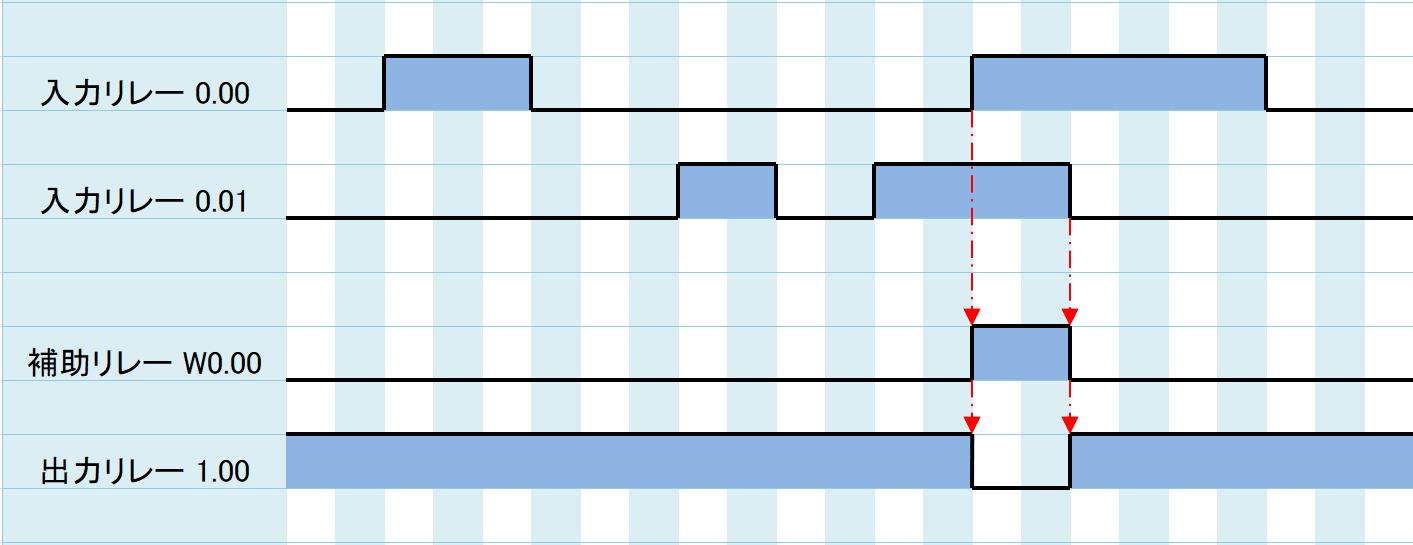
W0.00が0.00と0.01のAND(論理積)、1.00がNAND(否定論理積)となります。
W0.00を反転した結果が1.00となります。
タッチパネルの動作イメージ
タッチパネルの動作イメージは以下のようになります。
スイッチ(0.00)かつスイッチ(0.01)が、どちらも押された時のみランプ(1.00)が消灯します。
ラダープログラム
ラダープログラムは以下のようになります。
内部補助リレーW0.00の実行条件に入力リレー0.00と0.01を直列で接続することにより、W0.00には0.00と0.01のAND(論理積)の結果が格納されます。(1行目)
出力リレー1.00の実行条件をW0.00のb接点にすることで、W0.00を反転した結果が1.00に格納されます。つまり0.00と0.01のAND(論理積)のW0.00の反転であるNAND(否定論理積)が1.00に格納されます。(2行目)
2.【例題②】入力条件3ヶのNAND回路
下記仕様のラダープログラムを解説します。
スイッチが1ヶでも放されるとランプは点灯する。
スイッチは押すとON、ランプはONすると点灯するものとする。
【例題①】では入力条件であるスイッチが2ヶでしたが今回は3ヶです。少しややこしくなりますが考え方は同じです。
真理値表
真理値表は以下のようになります。
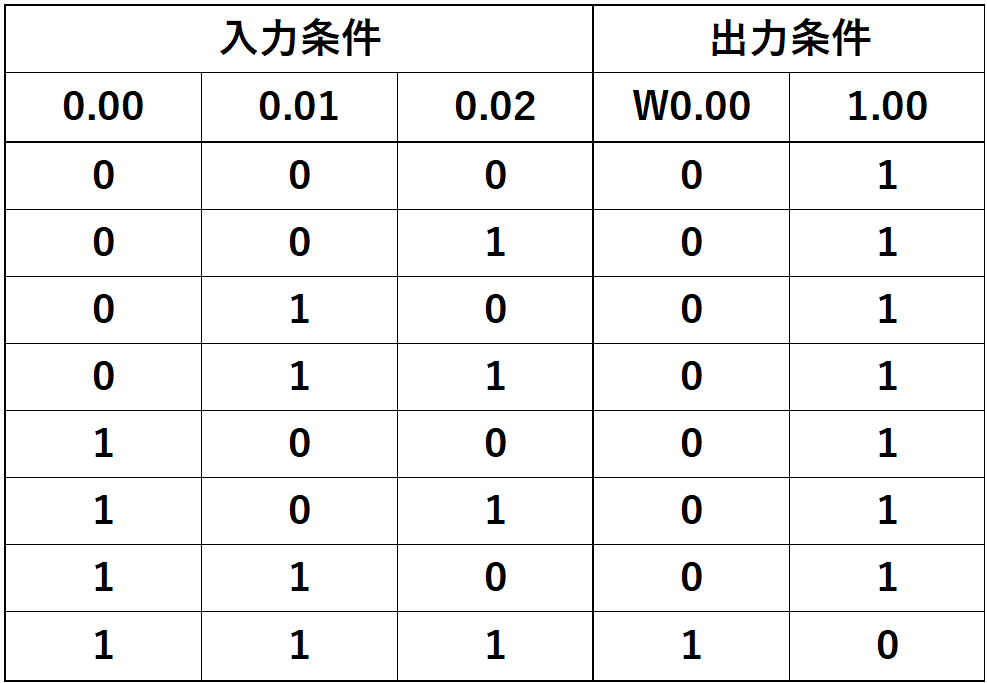
この真理値表では「”1”がON」「”0”がOFF」を表しています。
入力条件に対する「AND(論理積)がW0.00」「NAND(否定論理積)が1.00」となります。
タイムチャート
タイムチャートは以下のようになります。
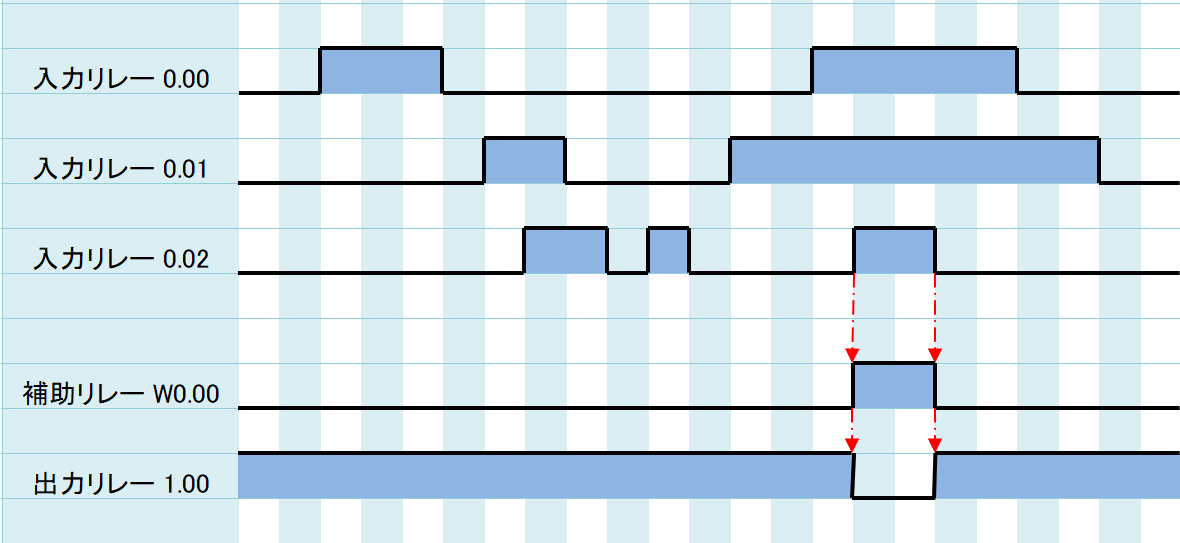
W0.00が0.00・0.01・0.02のAND(論理積)、1.00がNAND(否定論理積)となります。
W0.00を反転した結果が1.00となります。
タッチパネルの動作イメージ
タッチパネルの動作イメージは以下のようになります。
スイッチ(0.00)と(0.01)と(0.02)のすべてが押されたときのみ、ランプ(1.00)が消灯します。
ラダープログラム
ラダープログラムは以下のようになります。
NAND(否定論理積)回路の入力条件が増えた場合、AND(論理積)回路の入力条件に直列で追加します。
3. おわりに
オムロンCJシリーズで作成するNAND(否定論理積)回路のラダープログラム例を解説しました。
NAND(否定論理積)回路の動作は少々ややこしいかもしれませんが「AND回路の逆」と考えると簡単かもしれません。AND(論理積)回路は以下のページで解説しております。
【ラダープログラム回路】AND(論理積)回路のラダープログラム例【オムロンCJ】
よく似た名前で、NOR(否定論理和)回路と呼ばれるものが存在します。NOR(否定論理和)回路は以下のページで解説しております。
【ラダープログラム回路】NOR(否定論理和)回路のラダープログラム例【オムロンCJ】
電気ハード設計、PLC/タッチパネルソフト設計、ロボットティーチング、制御盤製作などの外注業務をご検討中の方は、ぜひ永工舎(エイコウシャ)にご相談ください。確かな技術と柔軟な対応で、現場の課題解決をサポートいたします。
当サイト「電気設計人.com」は個人事業主として永工舎を運営する永井が執筆しています。電気設計・制御設計に関する業務依頼やお見積もりも承っておりますので、お気軽にお問い合わせください。
シーケンス制御やラダープログラムの基礎から実務レベルまで、体系的に学べる良書をいくつか紹介します。どれも私自身が現場で役立ったと感じた参考書で、自信をもっておすすめできる内容です。
